изображений. Полученный инвариант называется уравнением Ла-гранжа – Гельмгольца. Рассмотрим изображение предмета y1 сис-темой из k сферических поверхностей (см. рис. 4.2). Из рисунка видно, что изображение y'1 отрезка y1 поверхностью 1 является предметом для преломляющей поверхности 2 и т.д. Изображение yk-1 является предметом для поверхности с номером k, т.е.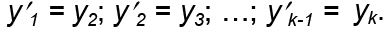
Показатели преломления n и углы , образуемые произвольным параксиальным лучом A1M1 с оптической осью имеют также двойные обозначения. Повторив вывод для второй поверхности, найдем выра-жение, аналогичное (4.13):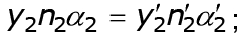
для поверхности с но-мером k получаем: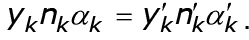
Полный инвариант Лагранжа-Гельмгольца для системы из k преломляющих поверхностей можно написать в следующем виде: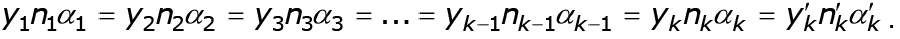
Страница: 1234567891011121314151617181920212223242526272829303132333435363738394041424344
4546474849505152535455565758596061626364656667686970717273747576777879808182838485
| Уход за глазамиФизикаНаука БейтсаТехнол.ФорумЛазер. коррек.Синя. под глаз.Зуд, жжения в глазахВраче. тайнаДр. болезни | |




