Выражение (4.6) носит название параксиального инварианта Аббе для сферической преломляющей поверхности. Инвариант Qs для двух сопряженных точек, находящихся на оптической оси, ве-личина постоянная, не зависящая от величины углов α и α' . Раскрыв скобки в выражении (4.6), запишем его в другой форме: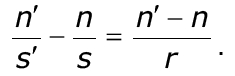



Выражение (4.7) называется уравнением параксиального луча для одной преломляющей поверхности. В формулу (4.7) не входит угол α (или высота h) луча с оптической осью. Это значит, что s' не зависит от α , т.е. все лучи, выходящие из точки предмета A под раз-личными, но обязательно малыми углами, после преломления прой-дут через одну и ту же точку A'. Положение распространяется и на центрированную систему, состоящую из нескольких преломляющих поверхностей, так как параксиальный луч остается близким к оптиче-ской оси на протяжении всего его хода через оптическую систему. От-сюда можно сделать вывод, что для реальных систем только в параксиальной области можно применять формулы и положе-ния, справедливые для идеальной оптической системы.

С изменением положения сопряженных точек A и A', величина инварианта Аббе будет изменяться. Величина инварианта Qs изменя-ется также при переходе от одной поверхности к другой, поэтому он не является полным инвариантом.

Из уравнения (4.7) можно найти фокусные расстояния одной преломляющей поверхности. Если луч падает на поверхность из бес-конечности, т.е.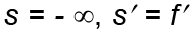



то, подставив эти значения в формулу (4.7) получим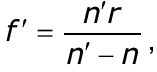



при подстановке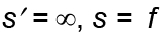



получим выражение для переднего фо-кусного расстояния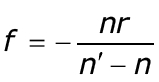



Разделив (4.8) на (4.9) получим зависимость между фокусными расстояниями одной преломляющей поверхности: