Однако измерения Птолемея относились к малым углам, и по-этому он пришел к неверному заключению о пропорциональности угла преломления углу падения.
Правильная формулировка закона преломления принадлежит Снеллиусу (1591 - 1626), указавшему в сочинении, оставшемся не-опубликованным, что отношение косекансов углов падения и прелом-ления остается постоянным, и Декарту, давшему в своем сочинении «Диоптрика» (1637 г.) современную формулировку закона преломле-ния. Декарт установил свой закон около 1630 г.; были ли ему известны исследования Снеллиуса – не известно. Закон преломления в форму-лировке Декарта гласил, что отношение синуса угла падения к синусу угла преломления есть величина постоянная: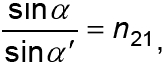



где n21 = n' / n называется относительным показателем прелом-ления.
Рассмотрим случай, когда свет распространяется из среды с большим показателем преломления в среду с меньшим показателем преломления. Из закона преломления (1.2) следует, что при n> n', преломленный луч удаляется от нормали, то есть угол преломления будет больше угла падения α> α' . Если увеличивать угол падения , то будет возрастать и угол преломления α', и, наконец, наступит мо-мент, когда угол преломления станет равным 90градусов, а sinɑ' равным еди-нице. В этом случае преломленный луч будет распространяться вдоль границы раздела двух сред. Дальнейшее увеличение угла падения приведет к тому, что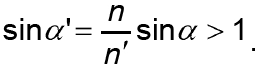



Синус угла преломления становится больше единицы, что противоре-чит определению синуса, и уравнение для угла преломления теряет смысл. Установлено, что в этом случае действительно не происходит преломления, а падающий луч полностью отражается от поверхности раздела в ту же среду, из которой он вышел. Это явление носит на-звание полного внутреннего отражения. Угол падения ɑс, которо-