Если –f = f, то из формул (2.17) и (2.18) находим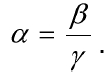



Формула (2.20) связывает увеличения оптической системы всех трех видов.

2.7. Соединение двух оптических систем в одну с общей осью симметрии

Оптические системы обычно состоят из нескольких отдельных частей, заданных положением главных плоскостей и фокусов. Систе-ма, действие которой эквивалентно действию заданных простых сис-тем с одной общей оптической осью, называется эквивалентной оптической системой. Чтобы найти эквивалентную оптическую систему, надо определить положение ее фокусов и главных плоско-стей.

Рассмотрим оптическую систему, состоящую из двух простых систем. На рис. 2.9. F1 и F'1; H1 и H'1 – точки фокусов и главные точки первой системы; F2 и F'2; H2 и H'2 – точки фокусов и главные точки второй системы. Взаимное расположение двух систем задается рас-стоянием d между задней главной плоскостью первой системы и пе-редней главной плоскостью второй системы. Иногда вместо расстоя-ния d задают расстояние от заднего фокуса первой оптической сис-темы до переднего фокуса второй системы, называемое оптическим интервалом ∆ (отрезок F'1F2 на рис. 2.9). Оптический интервал счи-тается положительным, если фокус F2 находится справа от фокуса F'1, и отрицательным – при обратном расположении этих точек. Как сле-дует из рис. 2.9, ∆> 0 и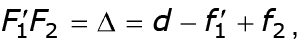



где f'1 и f2 – соответственно заднее фокусное расстояние первой сис-темы и передние фокусное расстояние второй системы.

Проведем произвольный луч PM1 параллельно оптической оси; он пересекает главные плоскости первой системы в точках M1 и M'1, проходит через ее задний фокус F'1, пересекает главные плоскости