мулу Ньютона, найдем отрезок zF по известному отрезку F'1F2 = ∆ (от-резок F'1F'2 отсчитывают от точки F'1):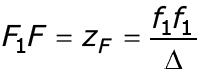
Определим фокусные расстояния f' и f эквивалентной системы. Из подобия треугольников P'H'F' и F'M'2H'2 следует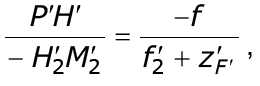
а из подобия треугольников H2M2F'1 и F'1H'1M'1 имеем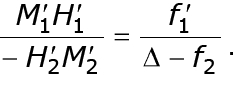
Так как для главных плоскостей β = 1, то H'2M'2 = H2M2, и по по-строению P'H'= M'1H'1, то правые части выражений (2.24) и (2.25) можно приравнять. В результате получим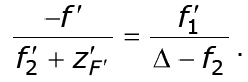
Подставим значение z'F, найденное из (2.22), в последнее вы-ражение, окончательно получим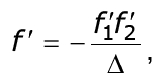
Путем аналогичных рассмотрений соответствующих треугольни-ков можно найти f. Так как треугольники PHF и FH1N1 подобны, то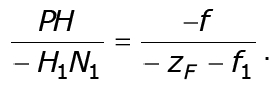
Из подобия треугольников HN'1F2 и F2N2H2 следует, что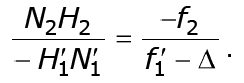
По построению PH = N2H2 и H1N1 = H'1N'1 , поэтому правые части двух последних выражений можно приравнять. После подстановки zF, найденного из (2.23), окончательно получим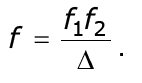
Страница: 1234567891011121314151617181920212223242526272829303132333435363738394041424344
4546474849505152535455565758596061626364656667686970717273747576777879808182838485
| Уход за глазамиФизикаНаука БейтсаТехнол.ФорумЛазер. коррек.Синя. под глаз.Зуд, жжения в глазахВраче. тайнаДр. болезни | |




