Подставим значения z и z' , найденные из (2.6) в (2.13). После уп-рощения будем иметь: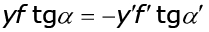
Выражение (2.14) носит название формулы или уравнения Ла-гранжа – Гельмгольца.
2.6. Угловое и продольное увеличение оптической системы. Их связь с линейным увеличением. Узловые точки
Угловым увеличением идеальной оптической системы называ-ется отношение тангенсов углов, образованных сопряженными лучами с оптической осью (рис. 2.6):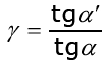
Из рис. 2.6 следует: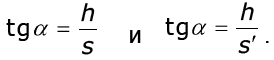
Подставляя значения tg ɑ и tg ɑ' в формулу (2.15), и принимая во внимание (2.11), получим: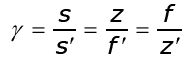
Воспользовавшись соотношениями (2.12) и (2.16), и получим за-висимость между угловым и линейным увеличениями: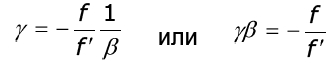
В частном случае, когда – f = f, формула (2.17) имеет вид γβ1. Формула (2.17) позволяет определить угловое увеличение в главных плоскостях. Так как линейное увеличение в главных плоскостях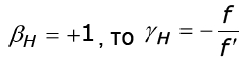
Страница: 1234567891011121314151617181920212223242526272829303132333435363738394041424344
4546474849505152535455565758596061626364656667686970717273747576777879808182838485
| Уход за глазамиФизикаНаука БейтсаТехнол.ФорумЛазер. коррек.Синя. под глаз.Зуд, жжения в глазахВраче. тайнаДр. болезни Porn. Порно ролики: https://www.ebooxa.com/categories/publichnoe-porno/. Порно онлайн бесплатно. | | |




