расстояний эквивалентной системы. Как видно из формул (2.28) и (2.29), главные точки эквивалентной системы также лежат на беско-нечно больших расстояниях: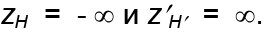



Системы, в которых оптический интервал равен нулю, называют-ся телескопическими или афокальными. Формула (2.30) линейного увеличения для телескопической системы имеет вид: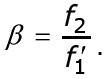



Из формулы (2.31) следует, что линейное увеличение телеско-пической системы постоянно и не зависит от положения сопряженных плоскостей, так как координата z1, характеризующая положение пред-мета относительно F1, в формулу не входит. Как видно из рис. 2.10, в телескопической системе всякий луч, параллельный оптической оси в пространстве предметов, например, луч BM1, выходит из системы па-раллельно оптической оси. Поэтому всякая точка, лежащая на линии BM1, изображается сопряженной ей точкой, на линии M'2B', т.е. отно-шение расстояний от сопряженных точек до оптической оси одинаково для всех пар таких точек ( β = const).