4.2. Инвариант Лагранжа – Гельмгольца для параксиальной области

В предыдущем параграфе было показано, что инвариант Аббе не является полным инвариантом. Существуют полные инварианты, которые сохраняют свое численное значение для всех (любого числа) поверхностей оптической системы.

Предположим, что отрезок AB, равный y (см. рис.4.1), после пре-ломления сферической поверхностью OM изображается отрезком A' B', длина которого равна y'. Из точки B направим луч на сфериче-скую поверхность по ее радиусу кривизны; так как угол падения такого луча равен нулю, то он пройдет поверхность без преломления.

Из подобия треугольников ABC и ABCследует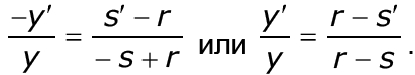



Из уравнения (4.6) найдем отношение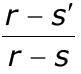



для чего предста-вим это уравнение в виде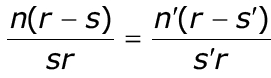



тогда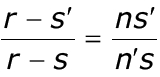



следовательно,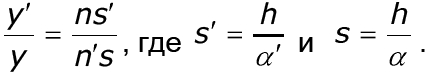



Заменив отношение s/s' отношением углов α/α', в результате получим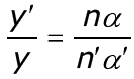



или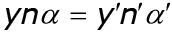



Выражение (4.13) имеет вид инварианта, так как оно показывает, что в параксиальной области произведение показателя преломления n, величины предмета y и угла α луча с осью в пространстве предме-тов равно произведению соответствующих величин в пространстве